Modeling with Numpy#
We will skip this notebook during the workshop. It demonstrates how to use numpy to prototype our mathematical model. For dynamic models, we strongly recommend prototyping in numpy, MATLAB, or a similar environment, especially if you are new to Pyomo. Once you are happy the model equations are reasonable, you can move to Pyomo.
The code below sets new defaults for plots.
import matplotlib.pyplot as plt
SMALL_SIZE = 14
MEDIUM_SIZE = 16
BIGGER_SIZE = 18
plt.rc('font', size=SMALL_SIZE) # controls default text sizes
plt.rc('axes', titlesize=SMALL_SIZE) # fontsize of the axes title
plt.rc('axes', labelsize=MEDIUM_SIZE) # fontsize of the x and y labels
plt.rc('xtick', labelsize=SMALL_SIZE) # fontsize of the tick labels
plt.rc('ytick', labelsize=SMALL_SIZE) # fontsize of the tick labels
plt.rc('legend', fontsize=SMALL_SIZE) # legend fontsize
plt.rc('figure', titlesize=BIGGER_SIZE) # fontsize of the figure title
plt.rc('lines', linewidth=3)
Numpy simulation#
import numpy as np
from scipy.integrate import solve_ivp
import pandas as pd
import matplotlib.pyplot as plt
# known parameters
T_amb = 21 # deg C
alpha = 0.00016 # watts / (units P1 * percent U1)
P1 = 200 # P1 units
# adjustable parameters
CpH = 7 # joules/deg C
CpS = 0.01 # joules/deg C
Ua = 0.05 # watts/deg C
Ub = 0.001 # watts/deg C
# initial conditions
TH1 = T_amb
TS1 = T_amb
IC = [TH1, TS1]
# input values
U1 = lambda t: 50 # steady state value of u1 (percent)
# extract data from experiment
t_expt = np.linspace(0, 600, 601)
def tclab_ode(theta, U1, T_amb, t_expt, return_data_frame=False):
'''ODE system for TCLab
Arguments:
theta: list fitted parameters CpH, CpS, Ua, Ub
U1: function that returns the value of U1 at time t
T_amb: ambient temperature
t_expt: time values for the experiment
'''
# unpack the adjustable parameters
Ua, Ub, inv_CpH, inv_CpS = theta
# right hand side of the ODEs
def deriv(t, y):
TH1, TS1 = y
dTH1 = (-Ua * (TH1 - T_amb) + Ub * (TS1 - TH1) + alpha * P1 * U1(t)) * inv_CpH
dTS1 = Ub * (TH1 - TS1) * inv_CpS
return [dTH1, dTS1]
# define the initial conditions
IC = [T_amb, T_amb]
# numerically integrate the ODEs
soln = solve_ivp(deriv, [min(t_expt), max(t_expt)], IC, t_eval=t_expt)
if return_data_frame:
# create dataframe with predictions
pred = pd.DataFrame(columns=["Time"])
pred["Time"] = t_expt
pred = pred.set_index("Time")
# report the model temperatures
pred["TH1"] = soln.y[0]
pred["TS1"] = soln.y[1]
# create dataframe with predictions
pred = pd.DataFrame(columns=["Time"])
pred["Time"] = t_expt
pred["TH1"] = soln.y[0]
pred["TS1"] = soln.y[1]
pred["Q1"] = U1(t_expt)
return pred
else:
return soln.y[1]
pred = tclab_ode(
theta=[Ua, Ub, 1 / CpH, 1 / CpS],
U1=U1,
T_amb=T_amb,
t_expt=t_expt,
return_data_frame=True,
)
pred
| Time | TH1 | TS1 | Q1 | |
|---|---|---|---|---|
| 0 | 0.0 | 21.000000 | 21.000000 | 50 |
| 1 | 1.0 | 21.227741 | 21.011029 | 50 |
| 2 | 2.0 | 21.453832 | 21.042602 | 50 |
| 3 | 3.0 | 21.678288 | 21.092596 | 50 |
| 4 | 4.0 | 21.901125 | 21.157645 | 50 |
| ... | ... | ... | ... | ... |
| 596 | 596.0 | 52.543808 | 52.551269 | 50 |
| 597 | 597.0 | 52.547056 | 52.550723 | 50 |
| 598 | 598.0 | 52.550280 | 52.550540 | 50 |
| 599 | 599.0 | 52.553480 | 52.550681 | 50 |
| 600 | 600.0 | 52.556658 | 52.551106 | 50 |
601 rows × 4 columns
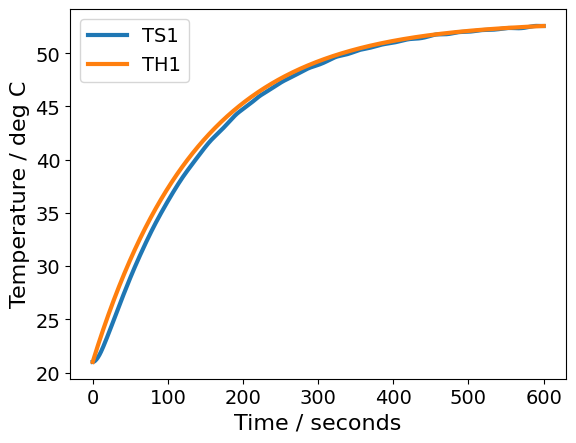
pred[["TS1", "TH1"]].plot(xlabel="Time / seconds", ylabel="Temperature / deg C")
plt.show()
Parameter estimation: step test#
Load data (step test)#
import sys
# If running on Google Colab, install Pyomo and Ipopt via IDAES
on_colab = "google.colab" in sys.modules
if on_colab:
file = "https://raw.githubusercontent.com/dowlinglab/pyomo-doe/main/data/tclab_step_test.csv'"
else:
file = '../data/tclab_step_test.csv'
df = pd.read_csv(file)
df.head()
| Time | T1 | T2 | Q1 | Q2 | |
|---|---|---|---|---|---|
| 0 | 0.00 | 22.84 | 22.84 | 50.0 | 0.0 |
| 1 | 1.00 | 22.84 | 22.84 | 50.0 | 0.0 |
| 2 | 2.01 | 23.16 | 22.84 | 50.0 | 0.0 |
| 3 | 3.02 | 22.84 | 22.84 | 50.0 | 0.0 |
| 4 | 4.01 | 22.84 | 22.84 | 50.0 | 0.0 |
Nonlinear regression and uncertainty analysis#
from scipy.optimize import least_squares
def covariance_to_correlation(cov):
'''Convert covariance matrix into correlation matrix
Argument:
cov: covariance matrix
Returns:
cor: correlation matrix
'''
# Copy matrix
cor = cov.copy()
# Get number of rows
n = cor.shape[0]
# Loop over rows
for r in range(n):
# Loop over columns
for c in range(n):
# Scale element
cor[r, c] = cor[r, c] / np.sqrt(cov[r, r] * cov[c, c])
return cor
def perform_regression(data, theta_initial=[Ua, Ub, 1 / CpH, 1 / CpS]):
'''Regress the data to find the parameters Ua, Ub, inv_CpH, inv_CpS
Arguments:
data: pandas DataFrame with columns "Time", "Q1", "T1", "T2"
theta_initial: initial guess for the parameters
'''
# Interpolate the control signal
U1 = lambda t: np.interp(t, data["Time"], data["Q1"])
# Calculate the initial conditions
T_amb = data.T1.values[0]
# Assemble y data
y_data = data["T1"].values
# Define residual function
def residuals(p):
pred = tclab_ode(p, U1, T_amb, data["Time"].to_numpy(), return_data_frame=False)
return pred - y_data
# Set bounds for Ua, Ub, inv_CpH, inv_CpS
# These are based on physical intuition
bnds = ([1e-5, 1e-5, 1e-2, 1e-2], [2.0, 2.0, 100, 100])
# Perform least squares nonlinear regression
nl_results = least_squares(
residuals, theta_initial, bounds=bnds, method='trf', verbose=2, loss="arctan"
)
theta_hat = nl_results.x
# extract and print values
Ua, Ub, inv_CpH, inv_CpS = nl_results.x
CpH = 1 / inv_CpH
CpS = 1 / inv_CpS
print('CpH = ', round(CpH, 3), "J/degC")
print('CpS =', round(CpS, 3), "J/degC")
print('Ua = ', round(Ua, 3), "W/degC")
print('Ub = ', round(Ub, 3), "W/degC")
# plot the results
pred = tclab_ode(
[Ua, Ub, inv_CpH, inv_CpS],
U1,
T_amb,
data["Time"].to_numpy(),
return_data_frame=True,
)
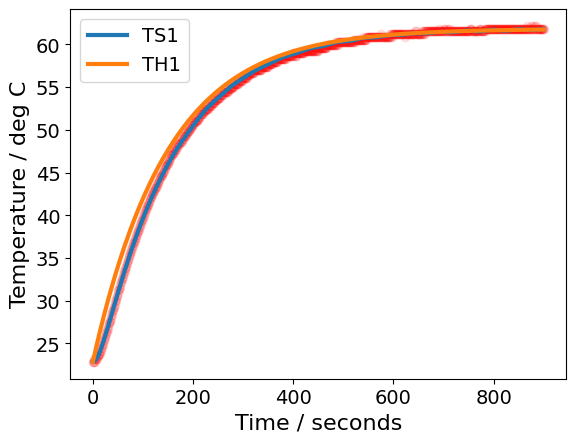
ax = data["T1"].plot(marker='o', color='red', alpha=0.1)
pred[["TS1", "TH1"]].plot(
ax=ax, linewidth=3, xlabel="Time / seconds", ylabel="Temperature / deg C"
)
plt.show()
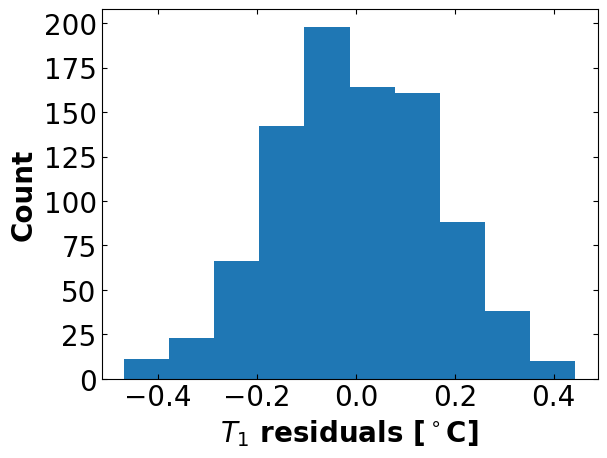
# plot the residuals
r = residuals(nl_results.x)
# define font size
fs = 20
# plot data
plt.hist(r)
plt.xlabel("$T_1$ residuals [$^\circ{}$C]", fontsize=fs, fontweight='bold')
plt.ylabel("Count", fontsize=fs, fontweight='bold')
# define tick size
plt.xticks(fontsize=fs)
plt.yticks(fontsize=fs)
plt.tick_params(direction="in", top=True, right=True)
# finish plot
plt.show()
# Estimate covariance and correlation of fitted parameters
# Estimate covariance of residuals
var_residuals = r.T @ r / (len(r) - len(nl_results.x))
print(
"Estimated standard deviation of residuals:",
round(np.sqrt(var_residuals), 3),
"deg C",
)
# Estimate covariance of fitted parameters
cov_p = var_residuals * np.linalg.inv(nl_results.jac.T @ nl_results.jac)
print("\nCovariance of p = [Ua, Ub, inv_CpH, inv_CpS]")
print(cov_p)
print("\nCorrelation matrix")
print(covariance_to_correlation(cov_p))
perform_regression(data=df)
Iteration Total nfev Cost Cost reduction Step norm Optimality
0 1 6.3133e+02 1.50e+05
1 2 5.8392e+02 4.74e+01 4.76e-02 5.82e+04
2 3 2.9743e+02 2.86e+02 9.82e+00 7.26e+05
3 6 2.6396e+02 3.35e+01 6.83e-03 2.92e+06
4 7 1.2592e+02 1.38e+02 1.94e-02 1.31e+06
5 8 5.2531e+01 7.34e+01 1.02e-02 5.77e+05
6 9 3.6753e+01 1.58e+01 3.20e-03 5.16e+05
7 10 2.5627e+01 1.11e+01 3.81e-03 3.35e+05
8 11 2.2790e+01 2.84e+00 9.23e-04 2.77e+05
9 12 2.0221e+01 2.57e+00 6.84e-04 3.79e+05
10 13 1.7188e+01 3.03e+00 2.96e-03 1.40e+05
11 14 1.6297e+01 8.91e-01 1.38e-03 1.72e+05
12 15 1.5026e+01 1.27e+00 4.06e-03 1.66e+05
13 16 1.3977e+01 1.05e+00 4.49e-03 1.10e+05
14 17 1.3596e+01 3.81e-01 3.11e-03 2.74e+04
15 18 1.3521e+01 7.53e-02 1.89e-03 1.41e+05
16 19 1.2610e+01 9.11e-01 6.17e-03 1.25e+05
17 20 1.2169e+01 4.41e-01 7.53e-03 1.00e+05
18 21 1.1888e+01 2.81e-01 9.23e-03 7.16e+04
19 22 1.1752e+01 1.36e-01 1.00e-02 4.45e+04
20 23 1.1703e+01 4.99e-02 1.49e-02 2.61e+04
21 24 1.1686e+01 1.65e-02 2.56e-02 1.49e+04
22 25 1.1681e+01 5.12e-03 4.75e-02 8.22e+03
23 26 1.1679e+01 1.50e-03 9.13e-02 4.41e+03
24 27 1.1679e+01 4.18e-04 9.93e-02 2.37e+03
25 28 1.1679e+01 1.16e-04 2.00e-01 1.31e+03
26 29 1.1679e+01 2.90e-05 4.03e-01 8.65e+02
27 30 1.1679e+01 9.37e-06 4.11e-01 6.12e+02
28 31 1.1679e+01 5.92e-06 1.05e-01 3.13e+02
29 32 1.1679e+01 1.49e-06 2.63e-02 1.66e+02
30 33 1.1679e+01 2.75e-07 6.58e-03 8.83e+01
31 40 1.1679e+01 0.00e+00 0.00e+00 8.83e+01
`xtol` termination condition is satisfied.
Function evaluations 40, initial cost 6.3133e+02, final cost 1.1679e+01, first-order optimality 8.83e+01.
CpH = 6.078 J/degC
CpS = 0.011 J/degC
Ua = 0.041 W/degC
Ub = 0.001 W/degC
Estimated standard deviation of residuals: 0.162 deg C
Covariance of p = [Ua, Ub, inv_CpH, inv_CpS]
[[ 8.69913569e-11 2.00596177e-10 8.45105896e-10 -2.50867485e-05]
[ 2.00596177e-10 4.21111809e-06 2.02824939e-06 -5.20161161e-01]
[ 8.45105896e-10 2.02824939e-06 9.98483655e-07 -2.50544262e-01]
[-2.50867485e-05 -5.20161161e-01 -2.50544262e-01 6.42508301e+04]]
Correlation matrix
[[ 1. 0.01048059 0.09067814 -0.01061126]
[ 0.01048059 1. 0.98912725 -0.99999963]
[ 0.09067814 0.98912725 1. -0.98917836]
[-0.01061126 -0.99999963 -0.98917836 1. ]]
Parameter estimation: sine test (poor initial guess)#
import sys
# If running on Google Colab, install Pyomo and Ipopt via IDAES
on_colab = "google.colab" in sys.modules
if on_colab:
file = "https://raw.githubusercontent.com/dowlinglab/pyomo-doe/main/data/tclab_sine_test_5min_period.csv"
else:
file = '../data/tclab_sine_test_5min_period.csv'
df2 = pd.read_csv(file)
df2.head()
| Time | T1 | T2 | Q1 | Q2 | |
|---|---|---|---|---|---|
| 0 | 0.00 | 22.2 | 22.2 | 50 | 0 |
| 1 | 1.01 | 22.2 | 22.2 | 51 | 0 |
| 2 | 2.01 | 22.2 | 22.2 | 52 | 0 |
| 3 | 3.00 | 22.2 | 22.2 | 53 | 0 |
| 4 | 4.01 | 22.2 | 22.2 | 54 | 0 |
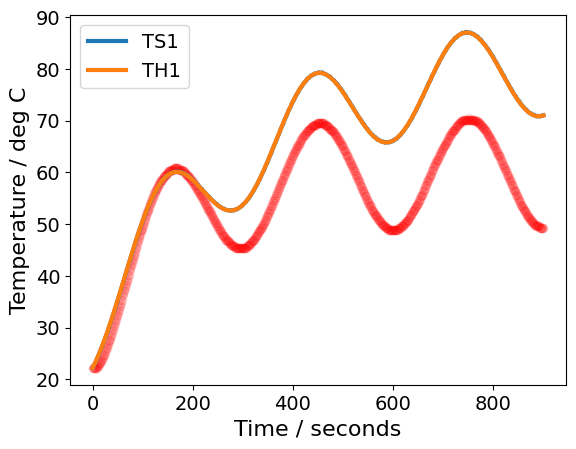
# Numpy is very sensitive to the initial guess
# With no initial theta, the values are quite far off
perform_regression(data=df2)
Iteration Total nfev Cost Cost reduction Step norm Optimality
0 1 6.3026e+02 5.84e+06
1 5 6.1654e+02 1.37e+01 4.24e-01 3.95e+05
2 6 6.0985e+02 6.69e+00 4.45e-02 2.64e+05
3 7 6.0831e+02 1.54e+00 3.60e-01 6.50e+04
4 8 6.0814e+02 1.71e-01 5.31e-02 8.62e+03
5 9 6.0800e+02 1.39e-01 5.61e-04 7.78e+02
6 14 6.0798e+02 1.47e-02 4.76e-05 2.80e+03
7 19 6.0798e+02 0.00e+00 0.00e+00 2.80e+03
`xtol` termination condition is satisfied.
Function evaluations 19, initial cost 6.3026e+02, final cost 6.0798e+02, first-order optimality 2.80e+03.
CpH = 8.354 J/degC
CpS = 0.01 J/degC
Ua = 0.026 W/degC
Ub = 0.029 W/degC
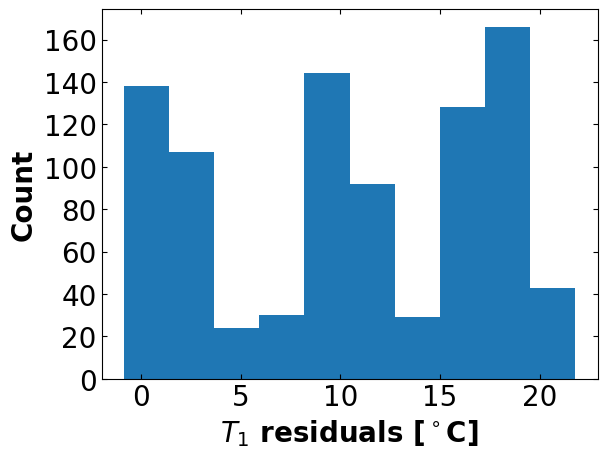
Estimated standard deviation of residuals: 12.569 deg C
Covariance of p = [Ua, Ub, inv_CpH, inv_CpS]
[[ 1.63875173e-04 2.10590923e-04 2.29570504e-04 -7.26559848e-01]
[ 2.10590923e-04 6.23920219e+01 3.16135832e-01 -2.13932132e+05]
[ 2.29570504e-04 3.16135832e-01 1.96281871e-03 -1.08398612e+03]
[-7.26559848e-01 -2.13932132e+05 -1.08398612e+03 7.33538653e+08]]
Correlation matrix
[[ 1. 0.00208266 0.40478034 -0.00209558]
[ 0.00208266 1. 0.90337715 -0.99999997]
[ 0.40478034 0.90337715 1. -0.90338344]
[-0.00209558 -0.99999997 -0.90338344 1. ]]
Parameter estimation: sine test (better initial guess)#
# Numpy is very sensitive to the initial guess
# With the step test optimal values, numpy gets fairly close
theta_initial = [0.041, 0.001, 1 / 6.078, 1 / 0.011] # Ua, Ub, inv_CpH, inv_CpS
perform_regression(data=df2, theta_initial=theta_initial)
Iteration Total nfev Cost Cost reduction Step norm Optimality
0 1 3.3475e+02 1.57e+08
1 2 3.3448e+02 2.70e-01 1.85e-05 2.09e+08
2 4 3.3352e+02 9.62e-01 9.38e-07 1.50e+08
3 5 3.3352e+02 0.00e+00 0.00e+00 1.50e+08
`xtol` termination condition is satisfied.
Function evaluations 5, initial cost 3.3475e+02, final cost 3.3352e+02, first-order optimality 1.50e+08.
CpH = 6.078 J/degC
CpS = 0.011 J/degC
Ua = 0.041 W/degC
Ub = 0.001 W/degC
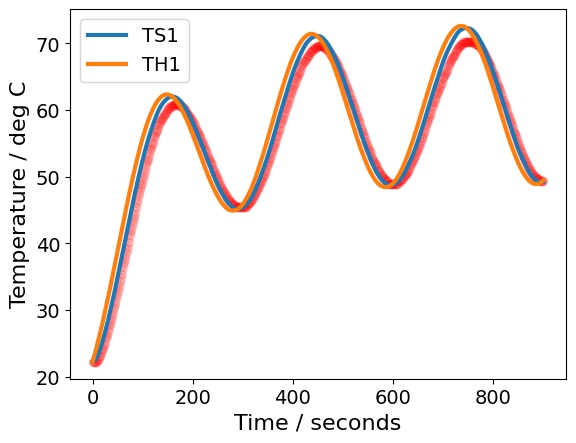
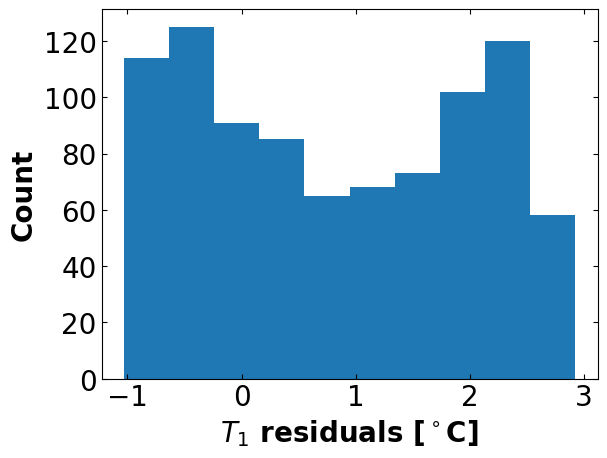
Estimated standard deviation of residuals: 1.437 deg C
Covariance of p = [Ua, Ub, inv_CpH, inv_CpS]
[[ 1.99483520e-14 -5.04688394e-16 -5.75632848e-15 -1.14001099e-12]
[-5.04688394e-16 3.98626401e-16 -1.56356528e-16 1.91168746e-14]
[-5.75632848e-15 -1.56356528e-16 5.02900388e-15 4.17152863e-14]
[-1.14001099e-12 1.91168746e-14 4.17152863e-14 1.34636028e-10]]
Correlation matrix
[[ 1. -0.17897269 -0.57471307 -0.69562452]
[-0.17897269 1. -0.11043125 0.08251886]
[-0.57471307 -0.11043125 1. 0.05069599]
[-0.69562452 0.08251886 0.05069599 1. ]]
Take Away Messasge#
Numpy is an excellent tool for rapidly prototyping models and performing basic parameter estimation. However, as we saw in this example, numpy was a little slow. Moreover, for the sine wave test, the least squares algorithm got stuck in local solutions. We will see soon how Pyomo is faster for optimization and often leads to more reliable parameter estimation solution.

