Pyomo.DoE: Exploratory Analysis#
import matplotlib.pyplot as plt
SMALL_SIZE = 14
MEDIUM_SIZE = 16
BIGGER_SIZE = 18
plt.rc('font', size=SMALL_SIZE) # controls default text sizes
plt.rc('axes', titlesize=SMALL_SIZE) # fontsize of the axes title
plt.rc('axes', labelsize=MEDIUM_SIZE) # fontsize of the x and y labels
plt.rc('xtick', labelsize=SMALL_SIZE) # fontsize of the tick labels
plt.rc('ytick', labelsize=SMALL_SIZE) # fontsize of the tick labels
plt.rc('legend', fontsize=SMALL_SIZE) # legend fontsize
plt.rc('figure', titlesize=BIGGER_SIZE) # fontsize of the figure title
plt.rc('lines', linewidth=3)
import sys
# If running on Google Colab, install Pyomo and Ipopt via IDAES
on_colab = "google.colab" in sys.modules
if on_colab:
!wget "https://raw.githubusercontent.com/dowlinglab/pyomo-doe/main/notebooks/tclab_pyomo.py"
# import TCLab model, simulation, and data analysis functions
from tclab_pyomo import (
TC_Lab_data,
TC_Lab_experiment,
extract_results,
extract_plot_results,
results_summary,
)
# set default number of states in the TCLab model
number_tclab_states = 2
Load experimental data (sine test)#
import pandas as pd
if on_colab:
file = "https://raw.githubusercontent.com/dowlinglab/pyomo-doe/main/data/tclab_sine_test_5min_period.csv"
else:
file = '../data/tclab_sine_test_5min_period.csv'
df = pd.read_csv(file)
df.head()
| Time | T1 | T2 | Q1 | Q2 | |
|---|---|---|---|---|---|
| 0 | 0.00 | 22.2 | 22.2 | 50 | 0 |
| 1 | 1.01 | 22.2 | 22.2 | 51 | 0 |
| 2 | 2.01 | 22.2 | 22.2 | 52 | 0 |
| 3 | 3.00 | 22.2 | 22.2 | 53 | 0 |
| 4 | 4.01 | 22.2 | 22.2 | 54 | 0 |
ax = df.plot(x='Time', y=['T1', 'T2'], xlabel='Time (s)', ylabel='Temperature (°C)')
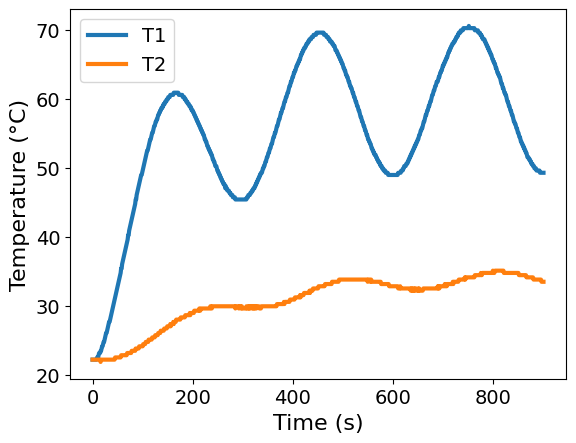
ax = df.plot(x='Time', y=['Q1', 'Q2'], xlabel='Time (s)', ylabel='Heater Power (%)')
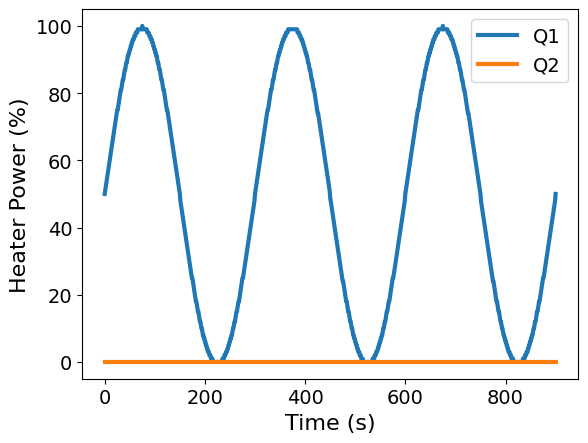
# Here, we will induce a step size of 6 seconds, as to not give too many
# degrees of freedom for experimental design.
skip = 6
# Create the data object considering the new control points every 6 seconds
tc_data = TC_Lab_data(
name="Sine Wave Test for Heater 1",
time=df['Time'].values[::skip],
T1=df['T1'].values[::skip],
u1=df['Q1'].values[::skip],
P1=200,
TS1_data=None,
T2=df['T2'].values[::skip],
u2=df['Q2'].values[::skip],
P2=200,
TS2_data=None,
Tamb=df['T1'].values[0],
)
Analyze FIM with Pyomo.DoE at initial point (sine test)#
# Load Pyomo.DoE class
from pyomo.contrib.doe import DesignOfExperiments
from pyomo.environ import SolverFactory
# Copied from previous notebook
theta_values = {
'Ua': 0.0417051733576387,
'Ub': 0.009440714239773074,
'inv_CpH': 0.1659093525658045,
'inv_CpS': 5.8357556063605465,
}
Reusing the Experiment object used for parameter estimation#
Recall that we utilized the experiment object during parameter estimation. From the Experiment Abstraction notebook, we labeled the important sets:
experiment_inputs- The experimental design decisions (control variables \(u_2\) in this case)experiment_outputs- The values measured during the experiment (temperature sensor data \(T_{S1}\) in this case)measurement_error- The error associated with individual values measured during the experimentunknown_parameters- Those parameters in the model that are estimated using the measured values during the experiment (heat transfer coefficients (\(U_a\) and \(U_b\)) and heat capacities (\(C^H_p\) and \(C^S_p\)) in this case)
This means we can use the same experiment object for optimal DoE! Therefore, we go about creating this object in the same way, except we will specify the values of the unknown parameters, \(\theta\).
# Create experiment object for design of experiments
doe_experiment = TC_Lab_experiment(data=tc_data, theta_initial=theta_values, number_of_states=number_tclab_states)
# Create the design of experiments object using our experiment instance from above
TC_Lab_DoE = DesignOfExperiments(experiment=doe_experiment,
step=1e-2,
scale_constant_value=1,
scale_nominal_param_value=True,
tee=True,)
FIM = TC_Lab_DoE.compute_FIM(method='sequential')
results_summary(FIM)
======Results Summary======
Four design criteria log10() value:
A-optimality: 5.773228885932493
D-optimality: 12.308607163946094
E-optimality: -1.793074158088514
Modified E-optimality: 7.514721752736364
FIM:
[[517225.40941304 1360.01262476 -66404.72541298 -1002.47319402]
[ 1360.01262476 5004.3737258 12379.2662576 5238.40389773]
[-66404.72541298 12379.2662576 65481.16908635 14190.01468139]
[ -1002.47319402 5238.40389773 14190.01468139 5526.94375493]]
eigenvalues:
[5.26802218e+05 6.26035823e+04 3.83207978e+03 1.61037063e-02]
eigenvectors:
[[-9.89752804e-01 -1.35949591e-01 4.36702406e-02 -7.52086327e-05]
[ 8.63262440e-04 -2.26164575e-01 -6.85698047e-01 -6.91857665e-01]
[ 1.42671125e-01 -9.31600001e-01 3.33329462e-01 -2.56487437e-02]
[ 5.79584008e-03 -2.49977462e-01 -6.45602485e-01 7.21578207e-01]]
We can see the FIM of the sine wave experiment is rank deficient with one eigenvalue that is numerically zero. We see the corresponding eigenvector points in the direction of the 2nd and 4th parameters, U_b and inv_CpS. This means the experiment alone does not contain enough information to uniquely estimate all of the parameters if the model.
Why does it make sense that \(U_b C_p^S\) is difficult to estimate?
Define parameterized sine wave experiment#
Can we further optimize the sine wave test to improve the information content? Let’s define the parameterized sine wave as:
where \(a\) is the amplitude (% power), \(p\) is the period (minutes), \(t\) is the time (seconds), and 60 is a conversion factor (seconds/minute).
Let’s look at the information content of \(p = 5\) minute and \(a = 50\) %.
# Create experiment object for design of experiments, now including the sine period and amplitude
sine_period = 5
sine_amplitude = 50
doe_experiment = TC_Lab_experiment(
data=tc_data,
theta_initial=theta_values,
number_of_states=number_tclab_states,
sine_amplitude=sine_amplitude,
sine_period=sine_period,
)
# Create the design of experiments object using our experiment instance from above
TC_Lab_DoE = DesignOfExperiments(experiment=doe_experiment,
step=1e-2,
scale_constant_value=1,
scale_nominal_param_value=True,
tee=True,)
FIM = TC_Lab_DoE.compute_FIM(method='sequential')
pyomo_doe_results = extract_plot_results(None, TC_Lab_DoE.compute_FIM_model)
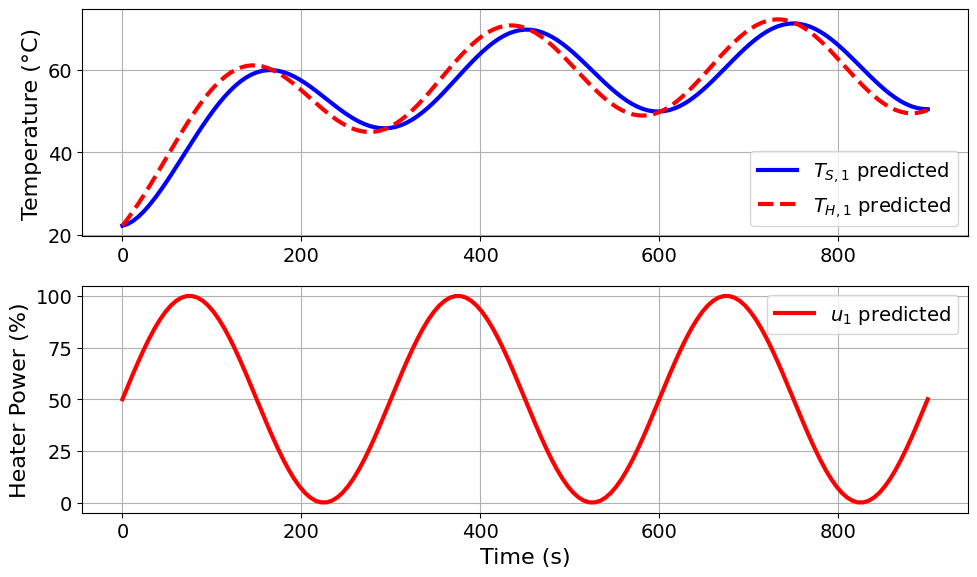
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 5 minutes
u1_amplitude = 50 % power
results_summary(FIM)
======Results Summary======
Four design criteria log10() value:
A-optimality: 5.780415236175106
D-optimality: 12.321221800291308
E-optimality: -1.7900021808076725
Modified E-optimality: 7.519483927119054
FIM:
[[526615.93104322 1269.39017779 -67742.74020183 -1135.81765702]
[ 1269.39017779 5002.22184096 12430.15508962 5238.07864931]
[-67742.74020183 12430.15508962 65988.9240756 14256.31640107]
[ -1135.81765702 5238.07864931 14256.31640107 5528.90185893]]
eigenvalues:
[5.36391326e+05 6.29165915e+04 3.82804512e+03 1.62180195e-02]
eigenvectors:
[[-9.89741606e-01 -1.36133505e-01 4.33499251e-02 -7.45344234e-05]
[ 1.03341873e-03 -2.25549256e-01 -6.85896472e-01 -6.91861616e-01]
[ 1.42740848e-01 -9.31879387e-01 3.32518176e-01 -2.56421659e-02]
[ 5.96112603e-03 -2.49391279e-01 -6.45831616e-01 7.21574652e-01]]
This parameterization reproduced the original sine wave experiment. As expected, the FIM is still rank deficient.
Perform sensitivity analysis to sine wave frequency and period#
Now let’s perform a sensitivity analysis over \(p\) and \(a\). Pyomo.DoE includes functions to automate this analysis including visualization. In our experience, an exploratory analysis like this is especially helpful to develop intuition about the physical system and model.
# Design variable ranges as lists
quick_run = False
if not quick_run:
# Larger sensitivity analysis with more detailed plots
design_ranges = {
"u1_period": [1, 2, 3, 4, 5, 6, 7, 8],
"u1_amplitude": [15, 25, 35, 45],
}
else:
# Faster sensitivity analysis, good for debugging
design_ranges = {"u1_period": [1, 2], "u1_amplitude": [20, 50]}
sensi_opt = "sequential_finite"
FIM_results = []
data_period = []
data_amplitude = []
count = 0
# Grid search
for period in design_ranges["u1_period"]:
for amplitude in design_ranges["u1_amplitude"]:
count += 1
print("=======Iteration Number: {} =======".format(count))
print("Design variable values for this iteration: (Period: {}, Amplitude: {})".format(period, amplitude))
data_period.append(period)
data_amplitude.append(amplitude)
doe_experiment = TC_Lab_experiment(
data=tc_data,
theta_initial=theta_values,
number_of_states=number_tclab_states,
sine_amplitude=amplitude,
sine_period=period,
)
# Create the design of experiments object using our experiment instance from above
TC_Lab_DoE = DesignOfExperiments(experiment=doe_experiment,
step=1e-2,
scale_constant_value=1,
scale_nominal_param_value=True,
tee=True,)
FIM = TC_Lab_DoE.compute_FIM(method='sequential')
pyomo_doe_results = extract_plot_results(None, TC_Lab_DoE.compute_FIM_model)
FIM_results.append(FIM)
=======Iteration Number: 1 =======
Design variable values for this iteration: (Period: 1, Amplitude: 15)
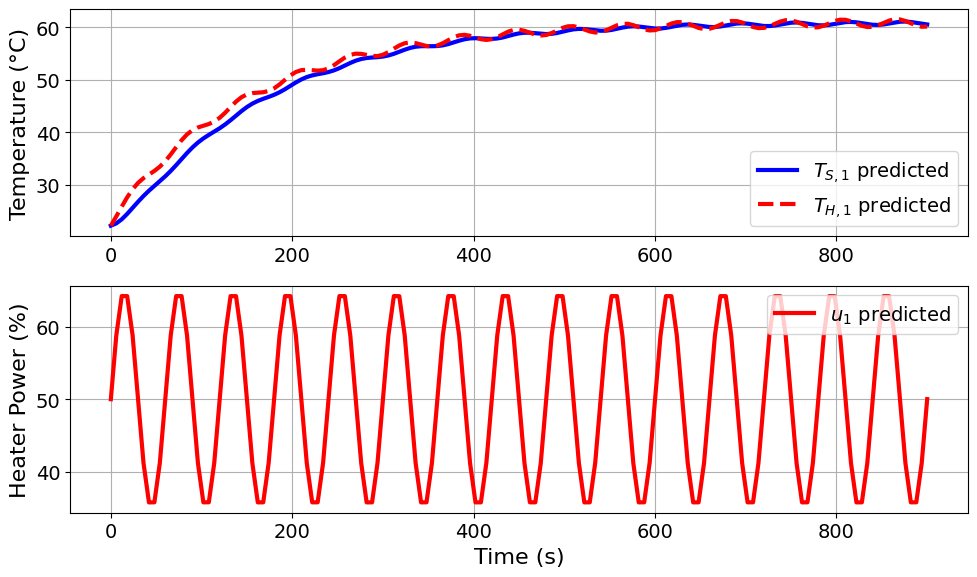
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 1 minutes
u1_amplitude = 15 % power
=======Iteration Number: 2 =======
Design variable values for this iteration: (Period: 1, Amplitude: 25)
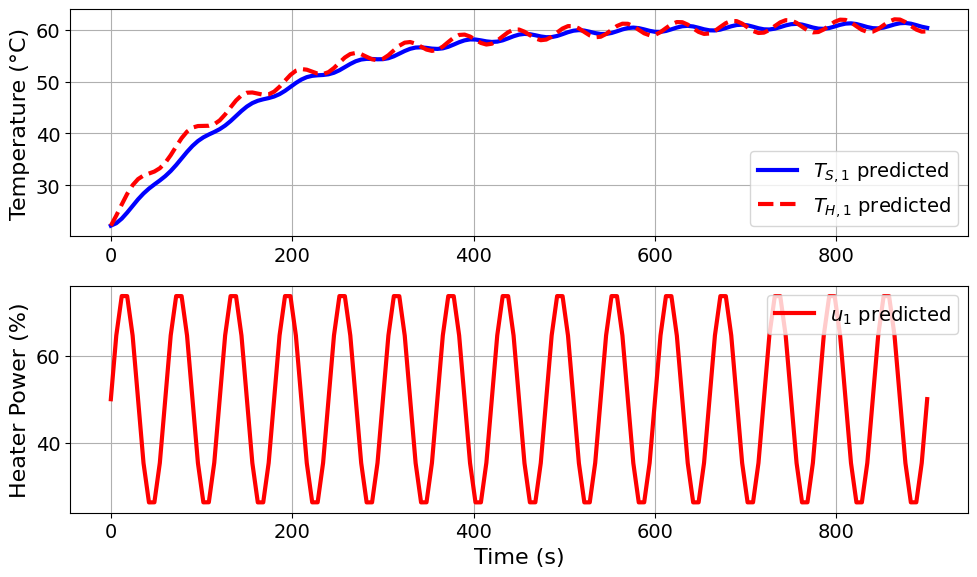
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 1 minutes
u1_amplitude = 25 % power
=======Iteration Number: 3 =======
Design variable values for this iteration: (Period: 1, Amplitude: 35)
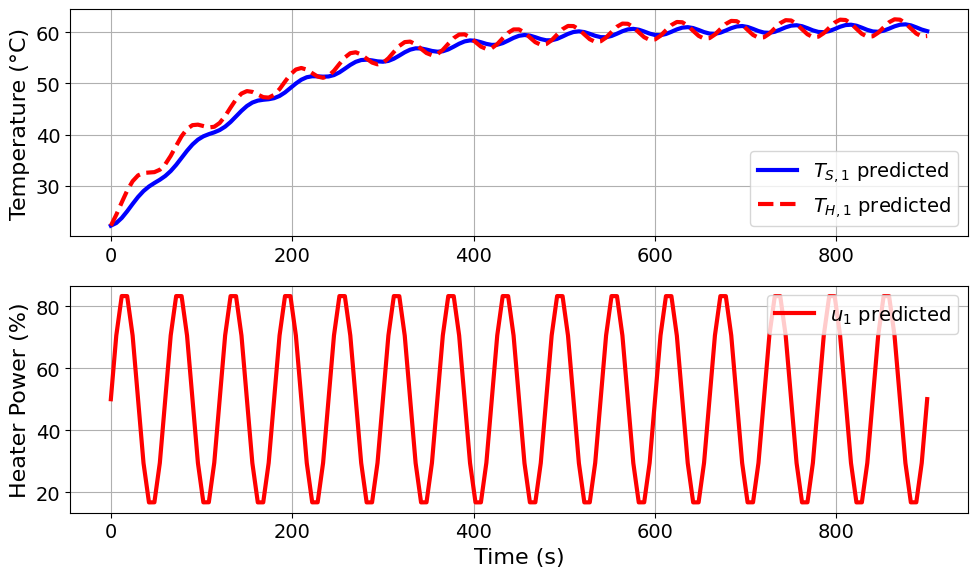
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 1 minutes
u1_amplitude = 35 % power
=======Iteration Number: 4 =======
Design variable values for this iteration: (Period: 1, Amplitude: 45)
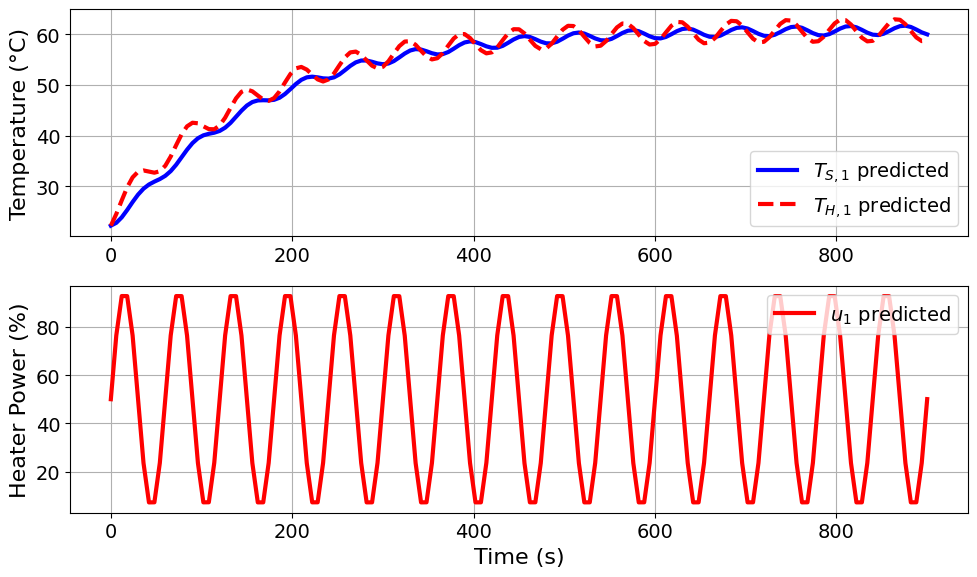
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 1 minutes
u1_amplitude = 45 % power
=======Iteration Number: 5 =======
Design variable values for this iteration: (Period: 2, Amplitude: 15)
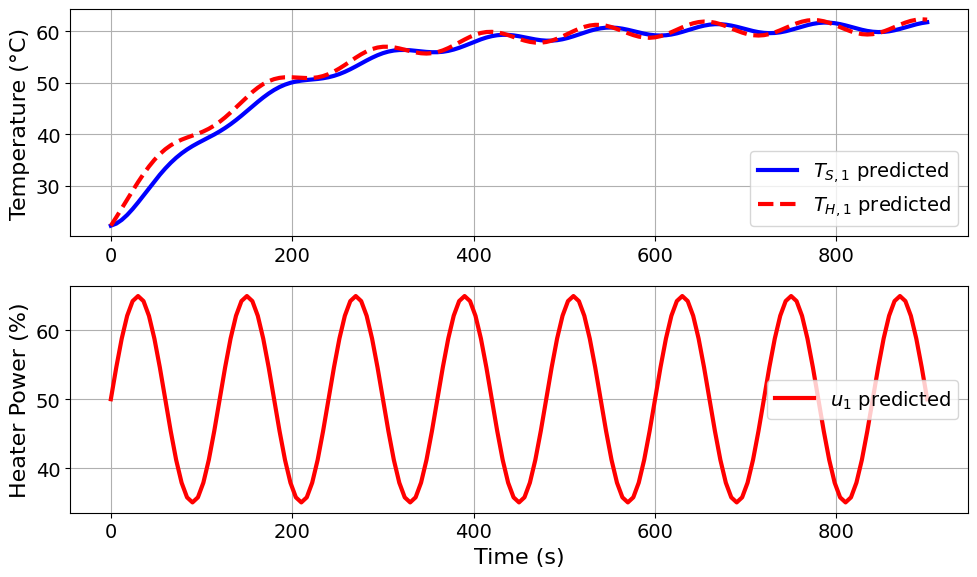
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 2 minutes
u1_amplitude = 15 % power
=======Iteration Number: 6 =======
Design variable values for this iteration: (Period: 2, Amplitude: 25)
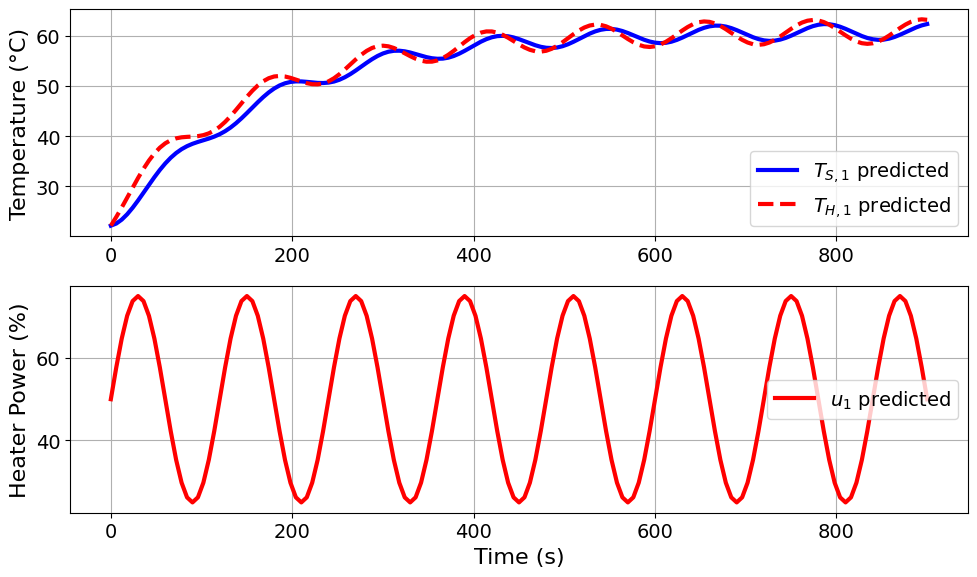
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 2 minutes
u1_amplitude = 25 % power
=======Iteration Number: 7 =======
Design variable values for this iteration: (Period: 2, Amplitude: 35)
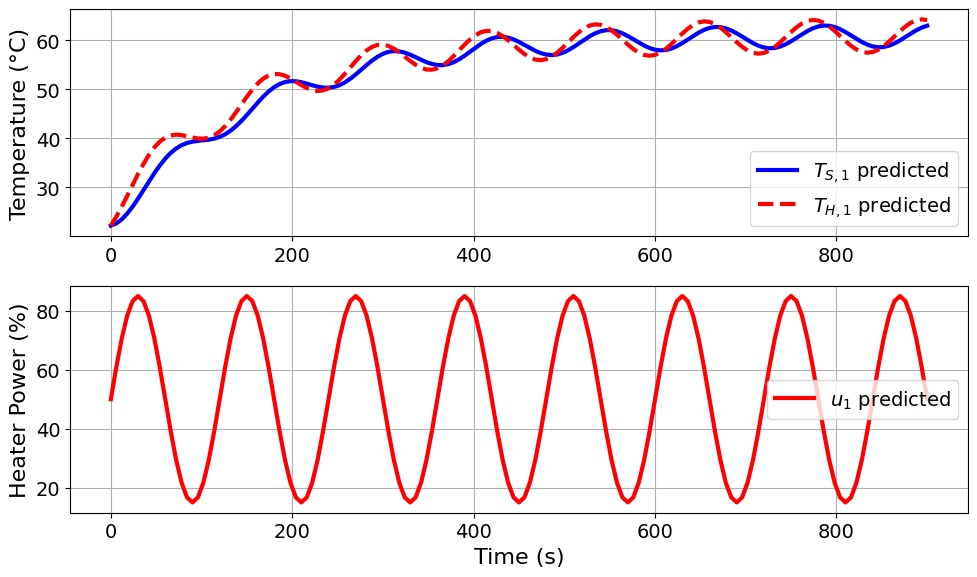
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 2 minutes
u1_amplitude = 35 % power
=======Iteration Number: 8 =======
Design variable values for this iteration: (Period: 2, Amplitude: 45)
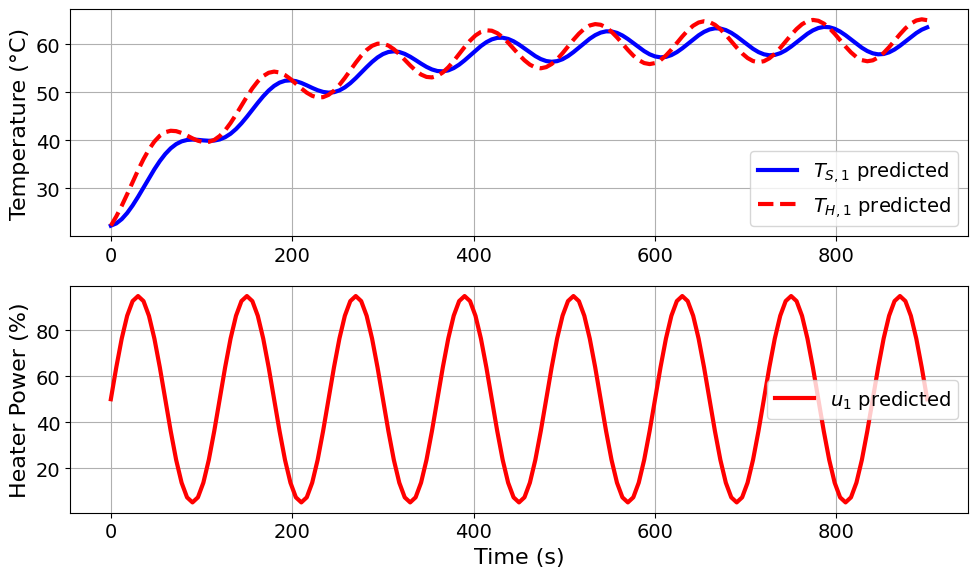
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 2 minutes
u1_amplitude = 45 % power
=======Iteration Number: 9 =======
Design variable values for this iteration: (Period: 3, Amplitude: 15)
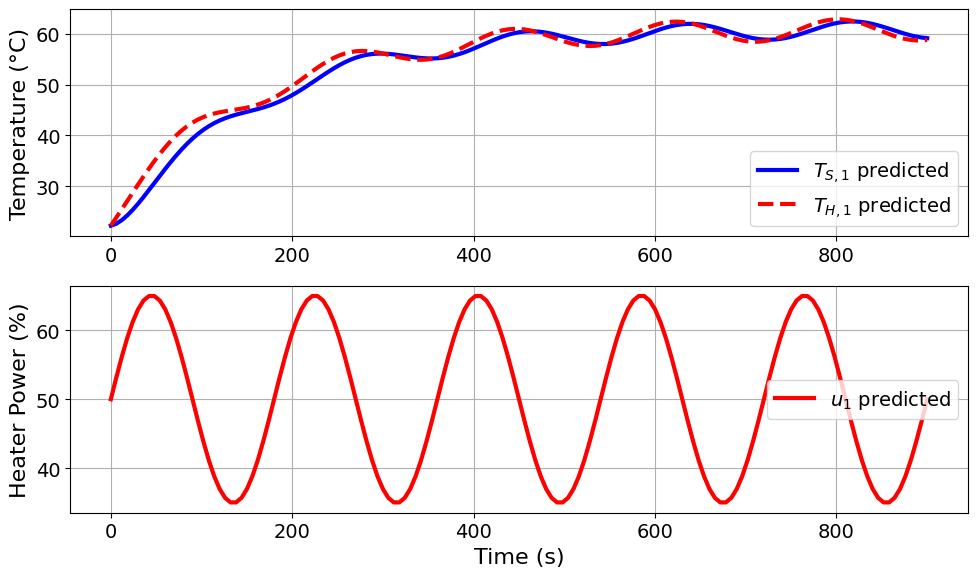
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 3 minutes
u1_amplitude = 15 % power
=======Iteration Number: 10 =======
Design variable values for this iteration: (Period: 3, Amplitude: 25)
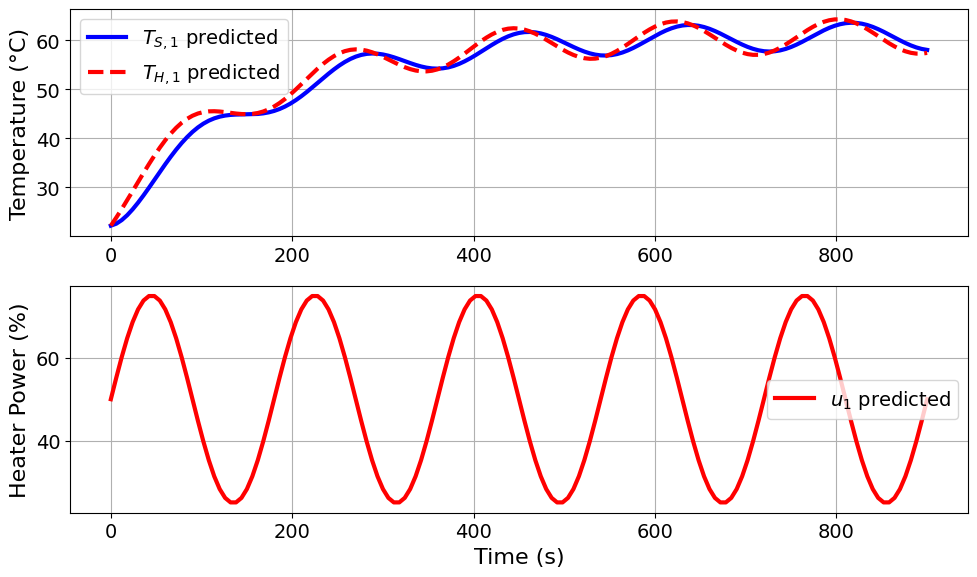
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 3 minutes
u1_amplitude = 25 % power
=======Iteration Number: 11 =======
Design variable values for this iteration: (Period: 3, Amplitude: 35)
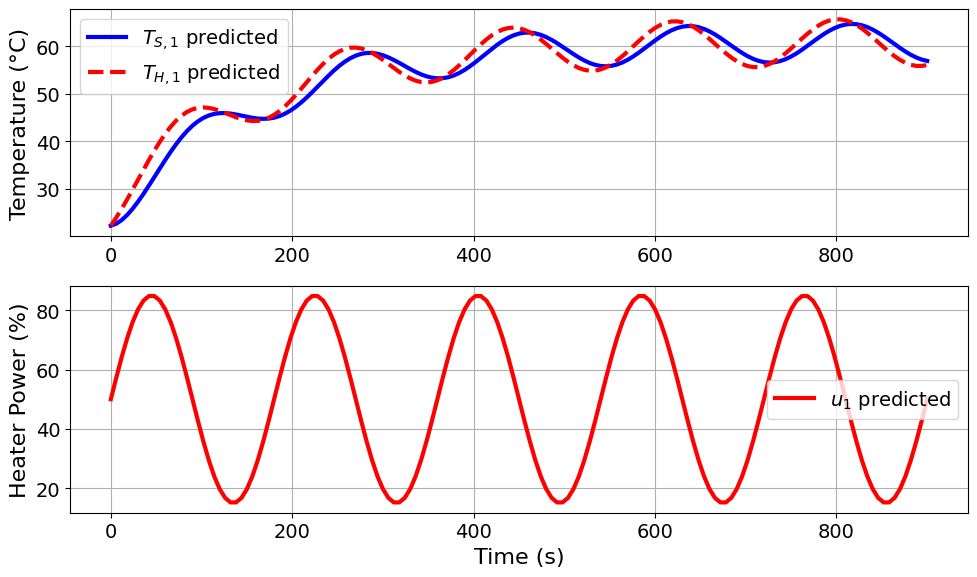
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 3 minutes
u1_amplitude = 35 % power
=======Iteration Number: 12 =======
Design variable values for this iteration: (Period: 3, Amplitude: 45)
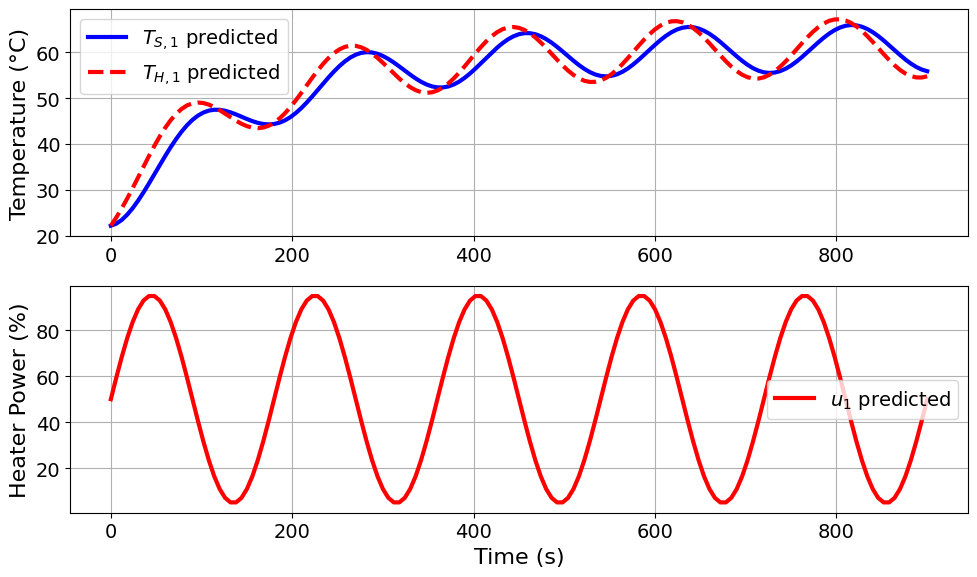
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 3 minutes
u1_amplitude = 45 % power
=======Iteration Number: 13 =======
Design variable values for this iteration: (Period: 4, Amplitude: 15)
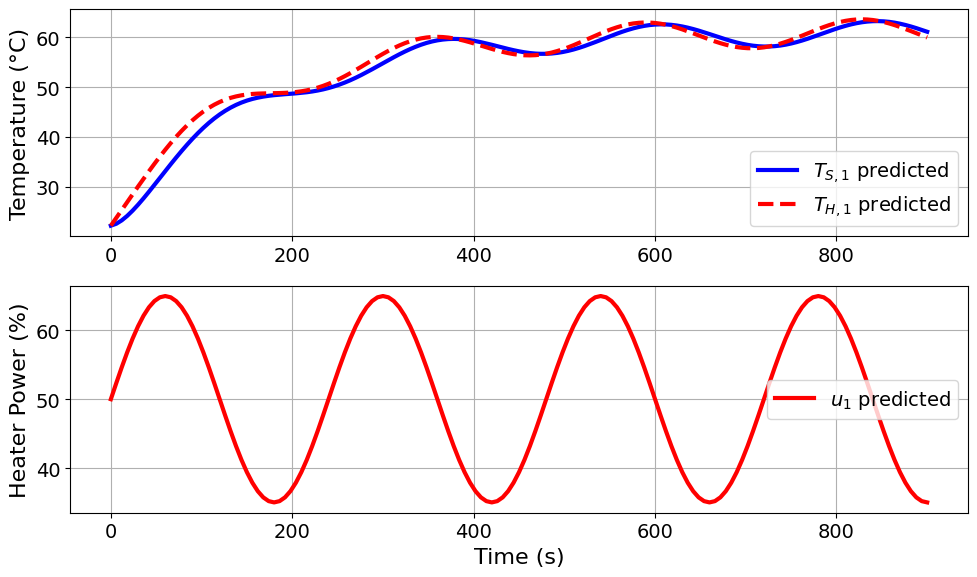
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 4 minutes
u1_amplitude = 15 % power
=======Iteration Number: 14 =======
Design variable values for this iteration: (Period: 4, Amplitude: 25)
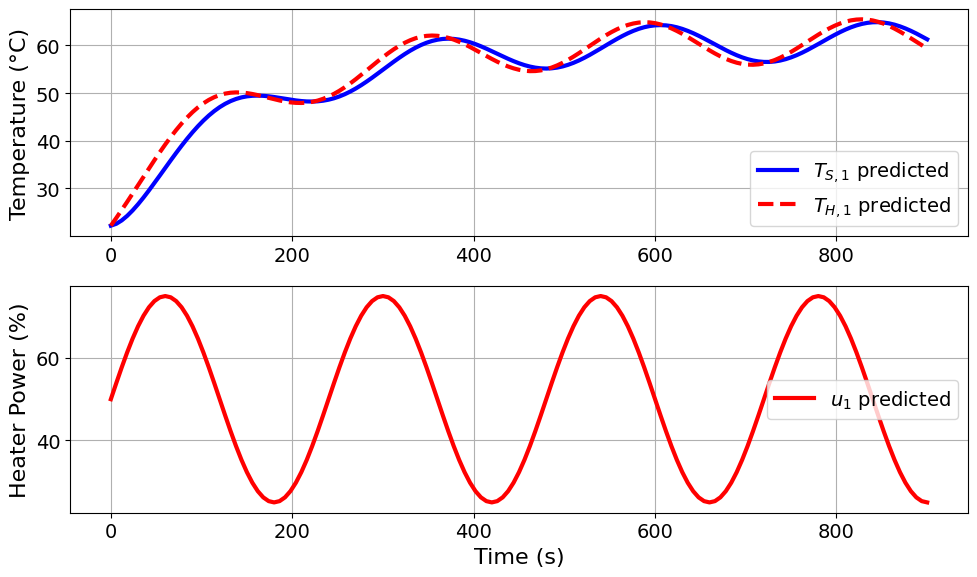
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 4 minutes
u1_amplitude = 25 % power
=======Iteration Number: 15 =======
Design variable values for this iteration: (Period: 4, Amplitude: 35)
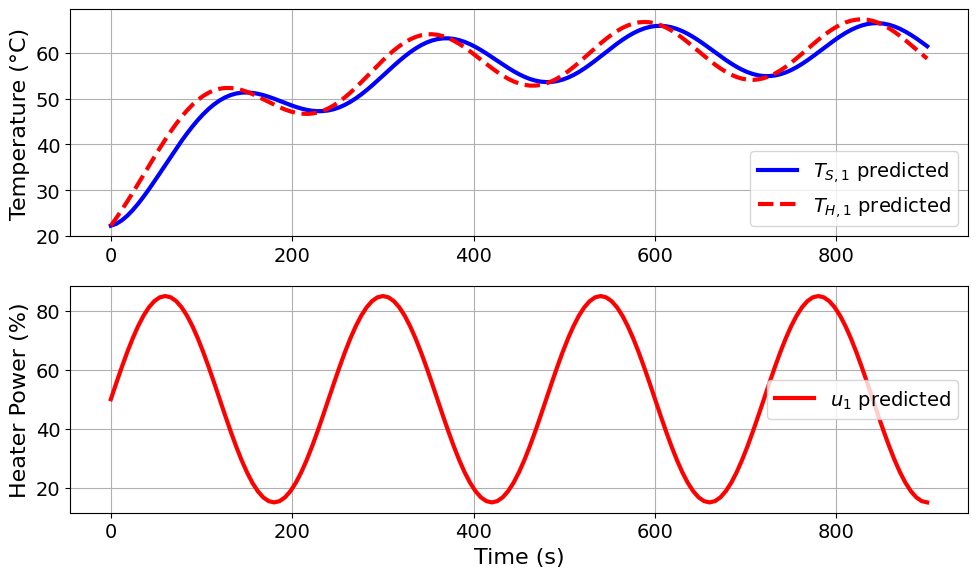
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 4 minutes
u1_amplitude = 35 % power
=======Iteration Number: 16 =======
Design variable values for this iteration: (Period: 4, Amplitude: 45)
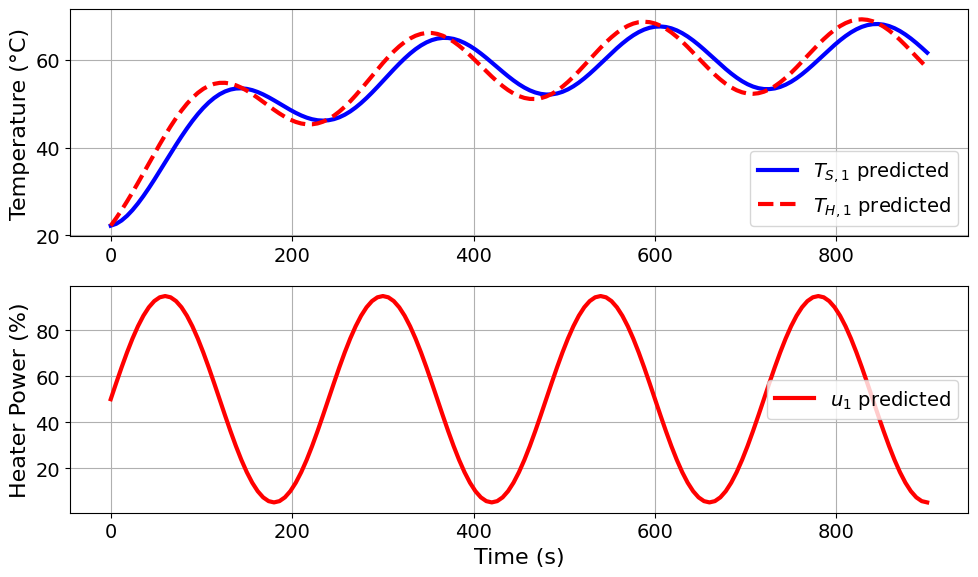
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 4 minutes
u1_amplitude = 45 % power
=======Iteration Number: 17 =======
Design variable values for this iteration: (Period: 5, Amplitude: 15)
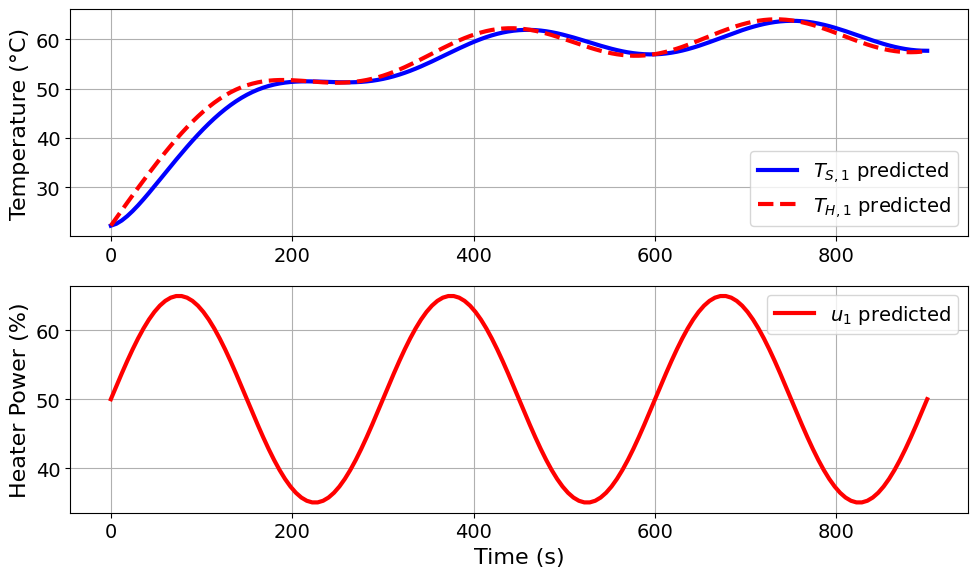
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 5 minutes
u1_amplitude = 15 % power
=======Iteration Number: 18 =======
Design variable values for this iteration: (Period: 5, Amplitude: 25)
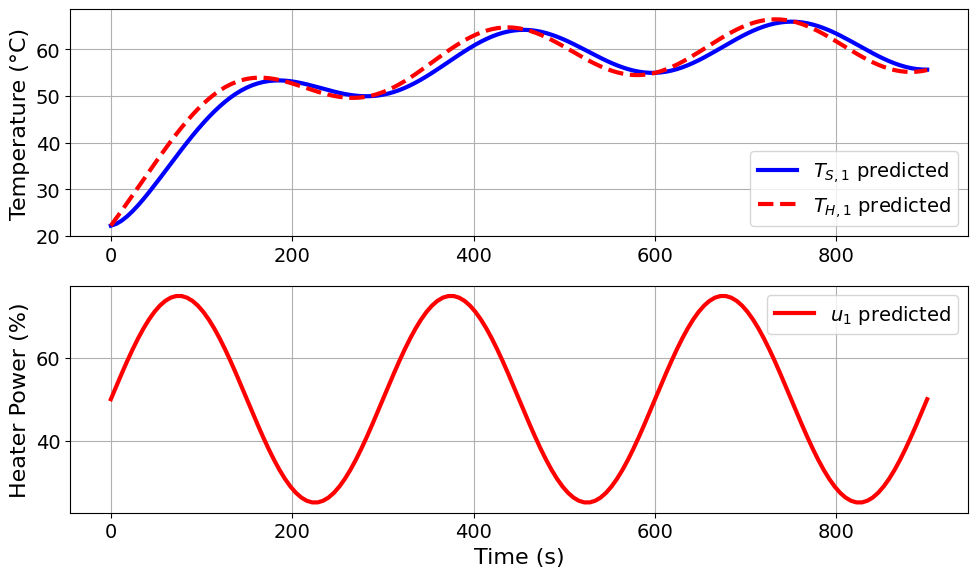
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 5 minutes
u1_amplitude = 25 % power
=======Iteration Number: 19 =======
Design variable values for this iteration: (Period: 5, Amplitude: 35)
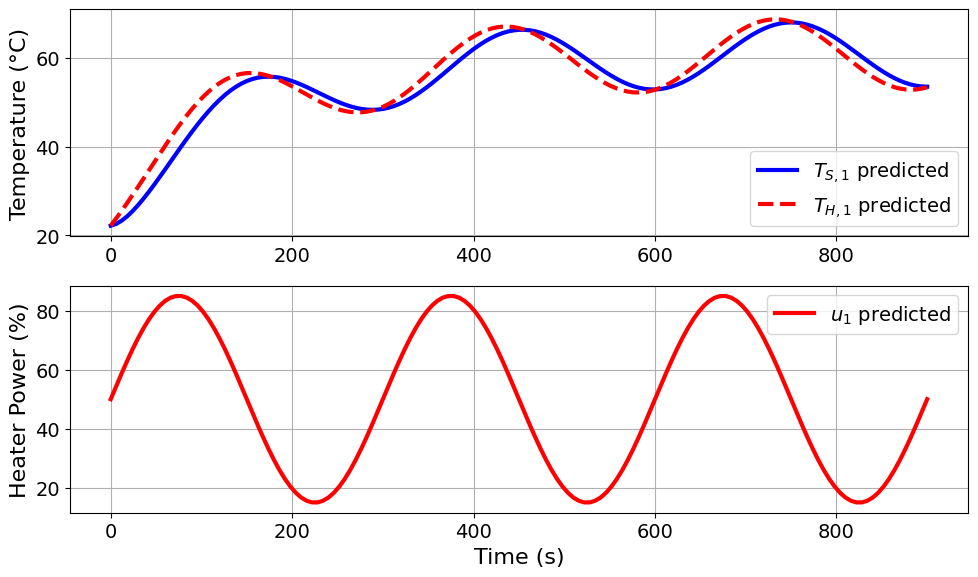
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 5 minutes
u1_amplitude = 35 % power
=======Iteration Number: 20 =======
Design variable values for this iteration: (Period: 5, Amplitude: 45)
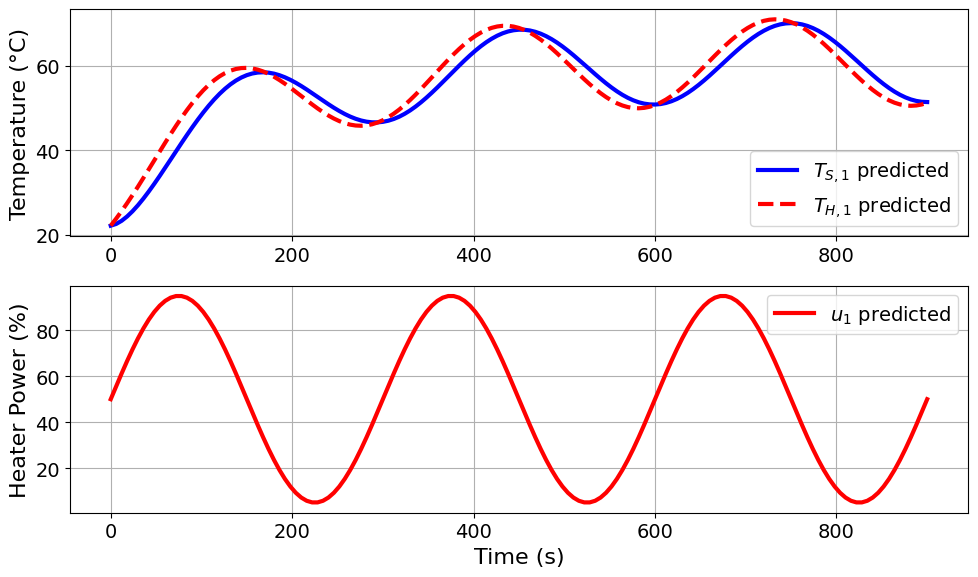
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 5 minutes
u1_amplitude = 45 % power
=======Iteration Number: 21 =======
Design variable values for this iteration: (Period: 6, Amplitude: 15)
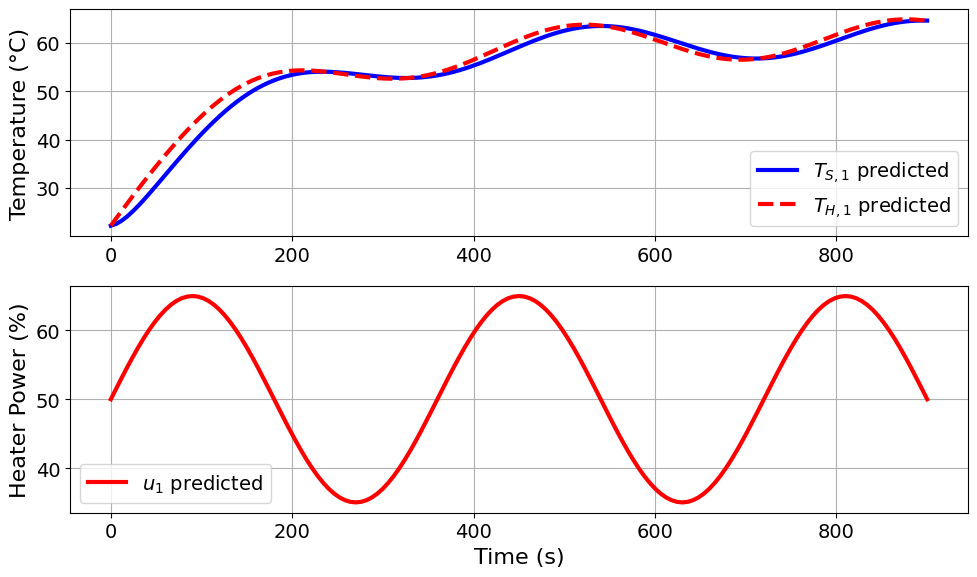
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 6 minutes
u1_amplitude = 15 % power
=======Iteration Number: 22 =======
Design variable values for this iteration: (Period: 6, Amplitude: 25)
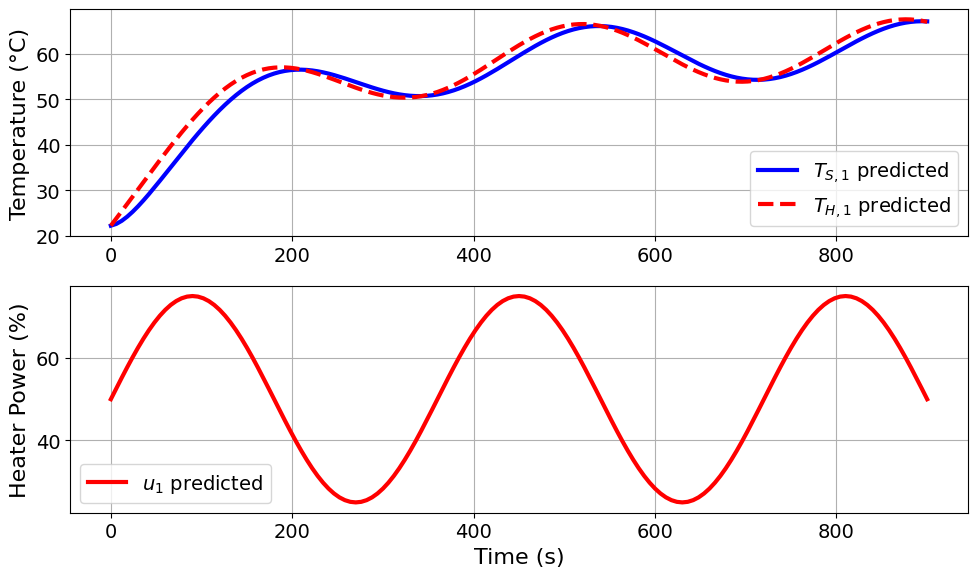
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 6 minutes
u1_amplitude = 25 % power
=======Iteration Number: 23 =======
Design variable values for this iteration: (Period: 6, Amplitude: 35)
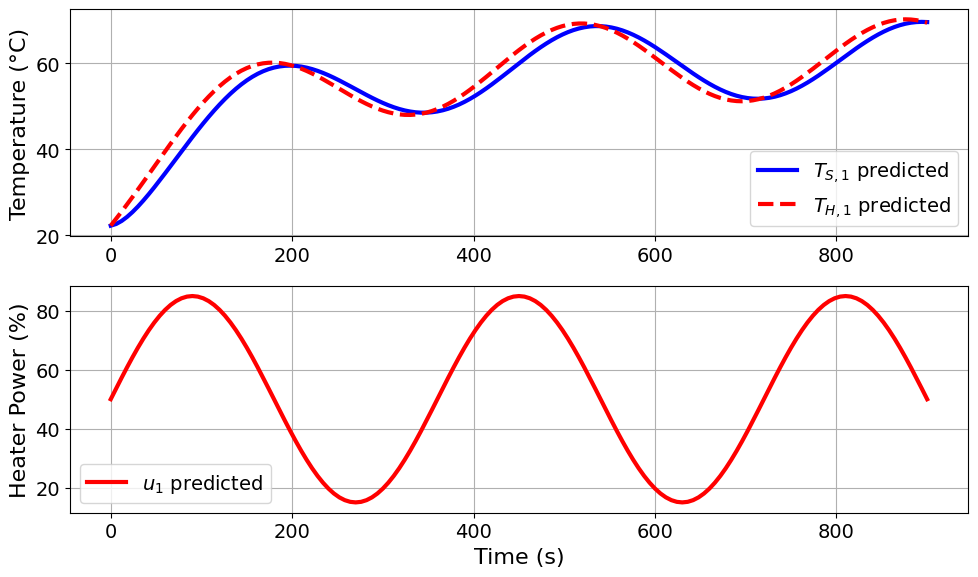
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 6 minutes
u1_amplitude = 35 % power
=======Iteration Number: 24 =======
Design variable values for this iteration: (Period: 6, Amplitude: 45)
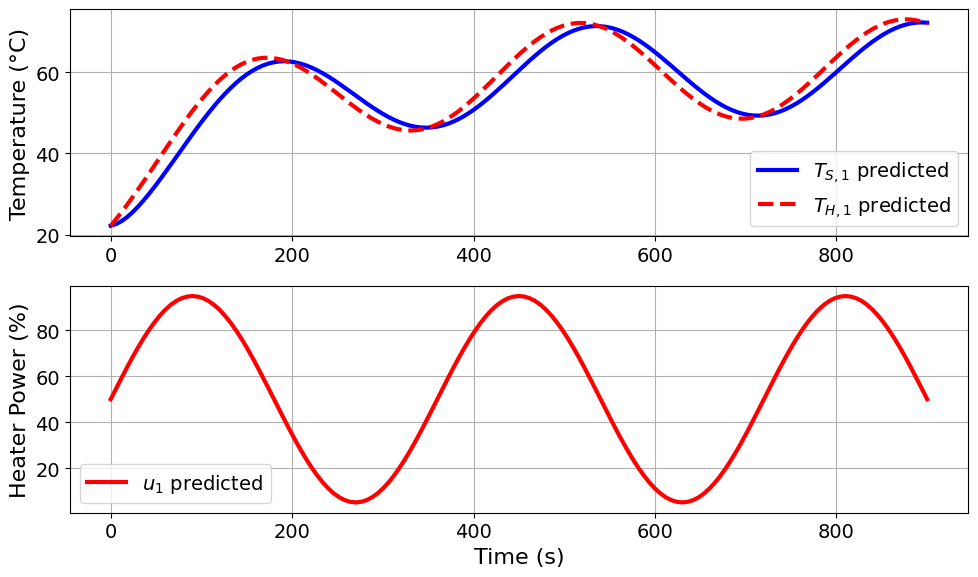
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 6 minutes
u1_amplitude = 45 % power
=======Iteration Number: 25 =======
Design variable values for this iteration: (Period: 7, Amplitude: 15)
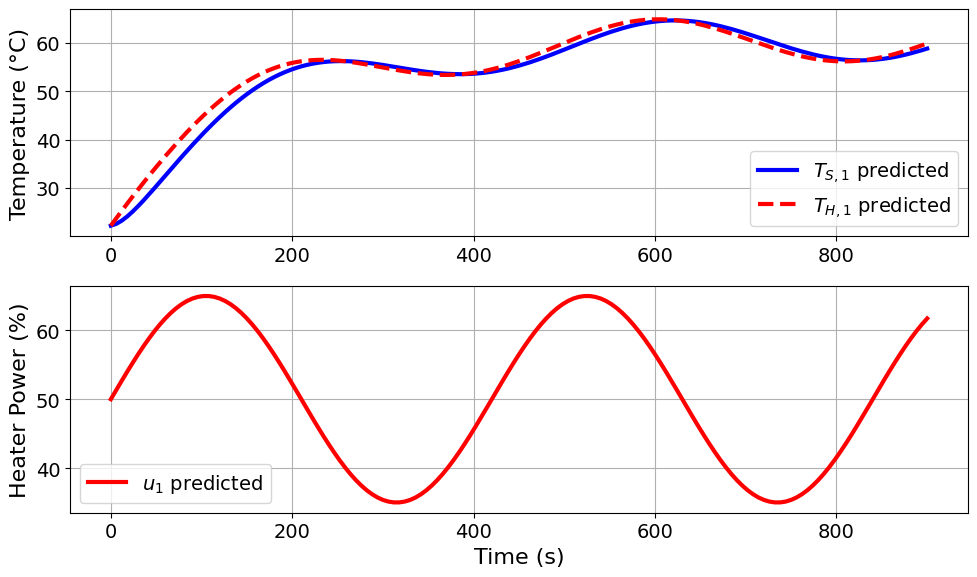
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 7 minutes
u1_amplitude = 15 % power
=======Iteration Number: 26 =======
Design variable values for this iteration: (Period: 7, Amplitude: 25)
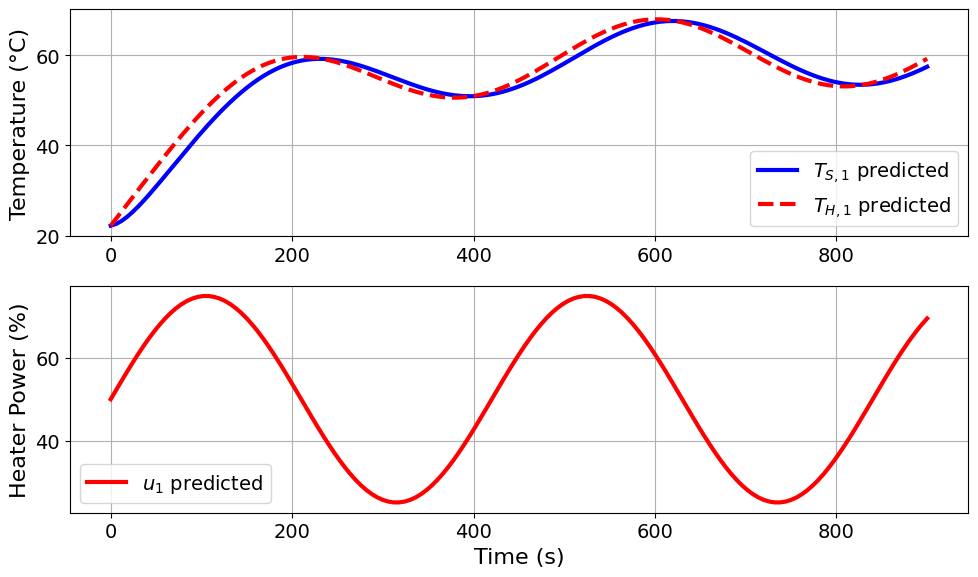
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 7 minutes
u1_amplitude = 25 % power
=======Iteration Number: 27 =======
Design variable values for this iteration: (Period: 7, Amplitude: 35)
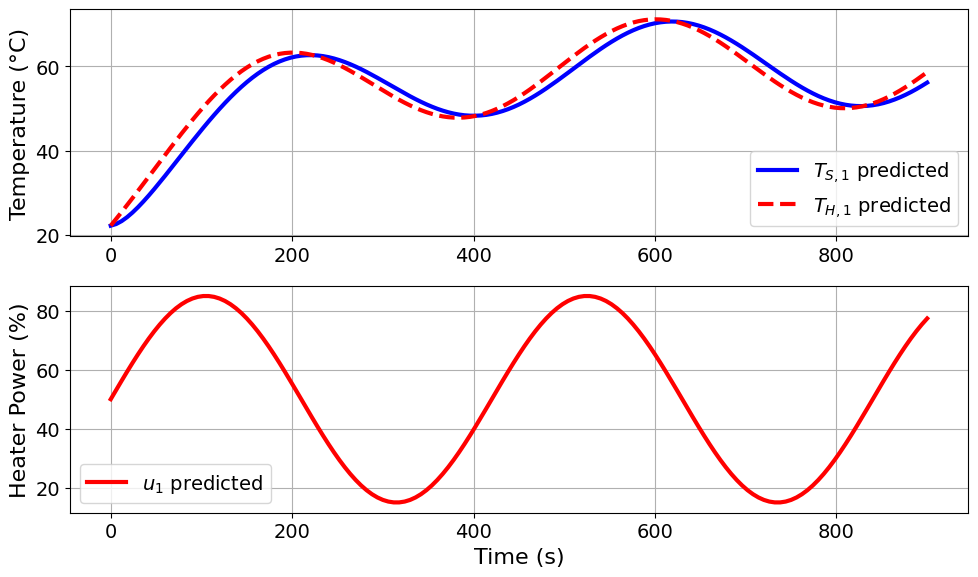
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 7 minutes
u1_amplitude = 35 % power
=======Iteration Number: 28 =======
Design variable values for this iteration: (Period: 7, Amplitude: 45)
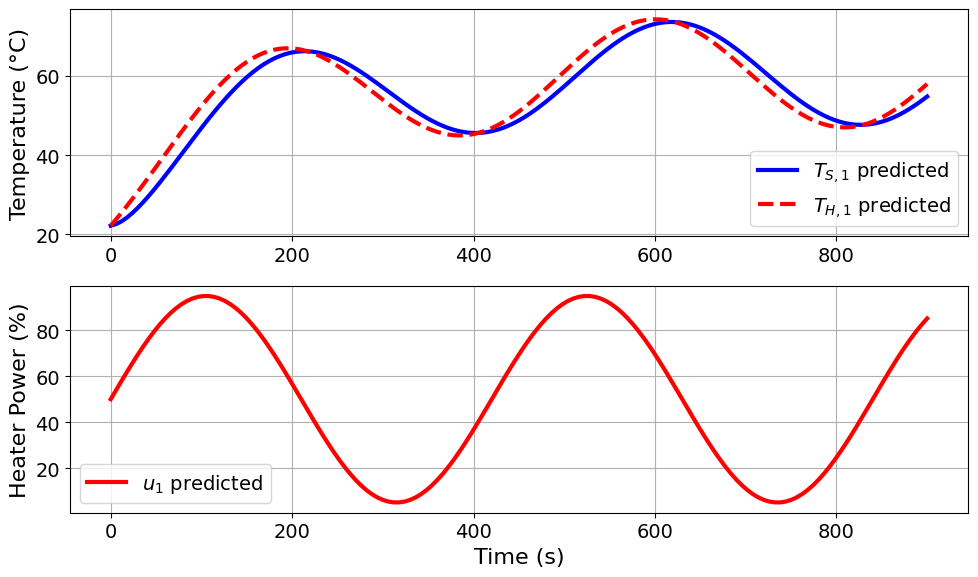
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 7 minutes
u1_amplitude = 45 % power
=======Iteration Number: 29 =======
Design variable values for this iteration: (Period: 8, Amplitude: 15)
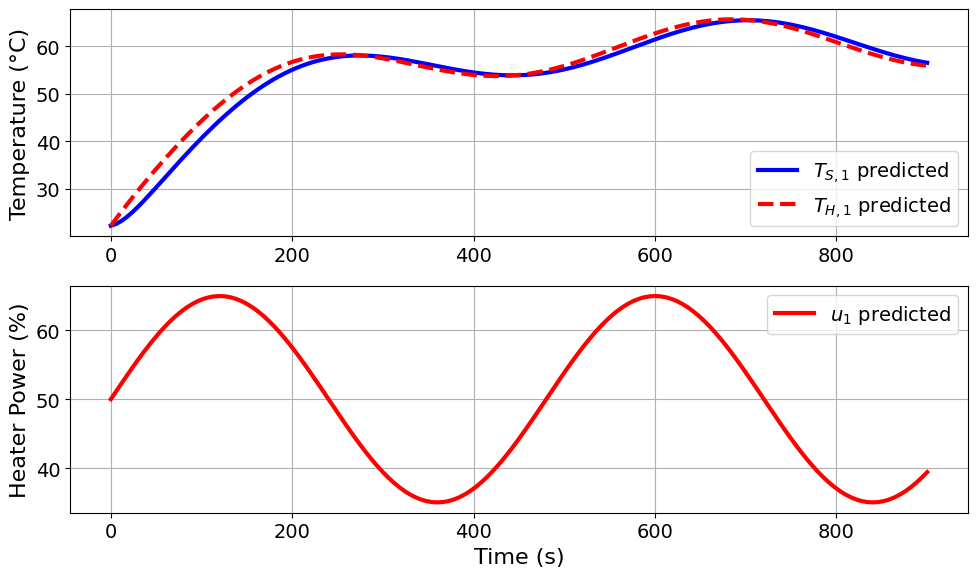
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 8 minutes
u1_amplitude = 15 % power
=======Iteration Number: 30 =======
Design variable values for this iteration: (Period: 8, Amplitude: 25)
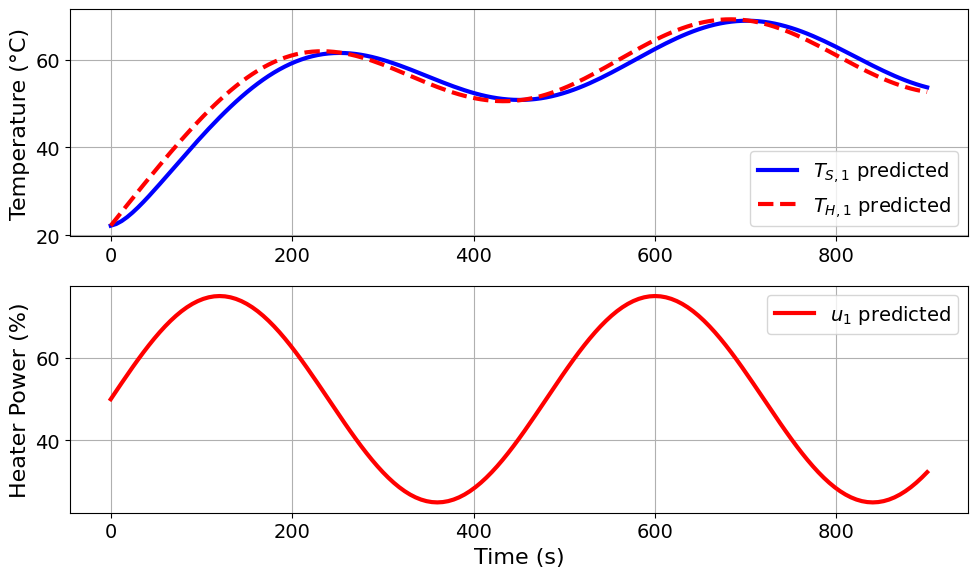
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 8 minutes
u1_amplitude = 25 % power
=======Iteration Number: 31 =======
Design variable values for this iteration: (Period: 8, Amplitude: 35)
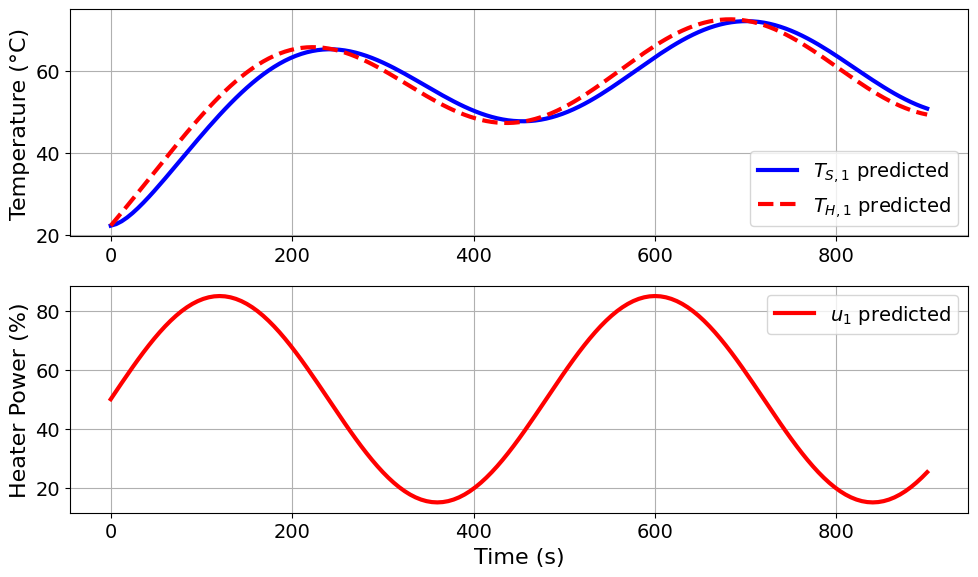
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 8 minutes
u1_amplitude = 35 % power
=======Iteration Number: 32 =======
Design variable values for this iteration: (Period: 8, Amplitude: 45)
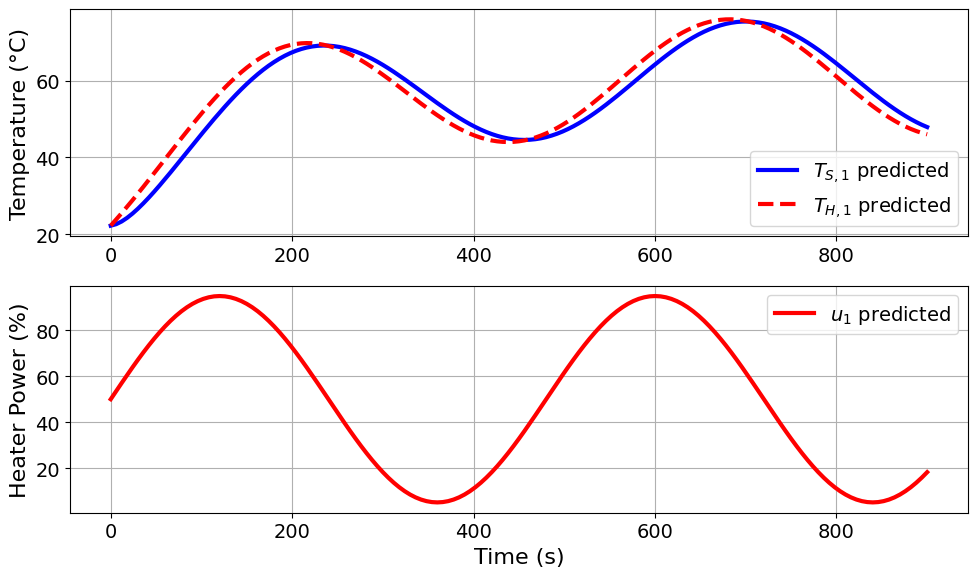
Model parameters:
Ua = 0.0413 Watts/degC
Ub = 0.0093 Watts/degC
CpH = 6.0883 Joules/degC
CpS = 0.1731 Joules/degC
u1_period = 8 minutes
u1_amplitude = 45 % power
Visualize and interpret sensitivity analysis results#
import numpy as np
# Extract criteria from FIM
def get_FIM_metrics(result):
eigenvalues, eigenvectors = np.linalg.eig(result)
min_eig = min(eigenvalues)
A_opt = np.log10(np.trace(result))
D_opt = np.log10(np.linalg.det(result))
E_opt = np.log10(min_eig)
ME_opt = np.log10(np.linalg.cond(result))
return A_opt, D_opt, E_opt, ME_opt
FIM_metrics = []
for i in FIM_results:
FIM_metrics.append(get_FIM_metrics(i))
FIM_metrics_np = np.asarray(FIM_metrics)
# Make heat map
def plot_heatmap(data, title, y_label, x_label, colorbar_label):
# set heatmap x,y ranges
x_tick_labels = np.sort(np.unique(data[:, 0]))
y_tick_labels = np.sort(np.unique(data[:, 1]))
# optimality-values
opt_vals = np.asarray(data[:, 2]).reshape(len(x_tick_labels), len(y_tick_labels))
# Plot the colormap
fig = plt.figure()
# Plotting options
ax = fig.add_subplot(111)
params = {"mathtext.default": "regular"}
plt.rcParams.update(params)
# Plotting data
ax.set_yticks(range(len(y_tick_labels)))
ax.set_yticklabels(y_tick_labels)
ax.set_ylabel(y_label)
ax.set_xticks(range(len(x_tick_labels)))
ax.set_xticklabels(x_tick_labels)
ax.set_xlabel(x_label)
im = ax.imshow(opt_vals.T, cmap=plt.cm.hot_r)
ba = plt.colorbar(im)
ba.set_label(colorbar_label)
plt.title(title)
# X and Y axis labels
x_label = "Period [min]"
y_label = "Amplitude [% power]"
# Draw A-optimality figure
data_A = np.zeros((len(FIM_metrics), 3))
data_A[:, 0] = data_period
data_A[:, 1] = data_amplitude
data_A[:, 2] = FIM_metrics_np[:, 0]
plot_heatmap(data_A, "Sine Wave Test: A-optimality", y_label, x_label, "log10(trace(FIM))")
# Draw D-optimality figure
data_D = np.zeros((len(FIM_metrics), 3))
data_D[:, 0] = data_period
data_D[:, 1] = data_amplitude
data_D[:, 2] = FIM_metrics_np[:, 1]
plot_heatmap(data_D, "Sine Wave Test: D-optimality", y_label, x_label, "log10(det(FIM))")
# Draw E-optimality figure
data_E = np.zeros((len(FIM_metrics), 3))
data_E[:, 0] = data_period
data_E[:, 1] = data_amplitude
data_E[:, 2] = FIM_metrics_np[:, 2]
plot_heatmap(data_E, "Sine Wave Test: E-optimality", y_label, x_label, "log10(min-eig(FIM))")
# Draw ME-optimality figure
data_ME = np.zeros((len(FIM_metrics), 3))
data_ME[:, 0] = data_period
data_ME[:, 1] = data_amplitude
data_ME[:, 2] = FIM_metrics_np[:, 3]
plot_heatmap(data_ME, "Sine Wave Test: ME-optimality", y_label, x_label, "log10(cond(FIM))")
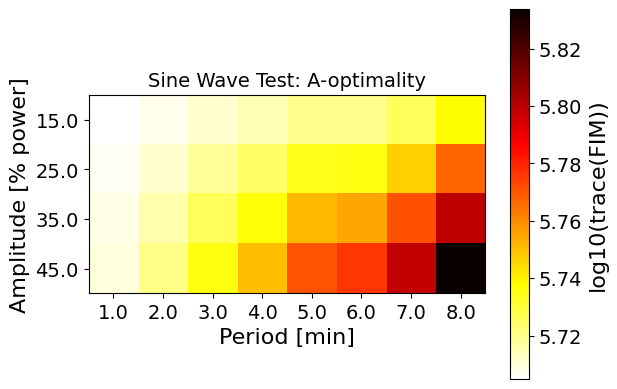
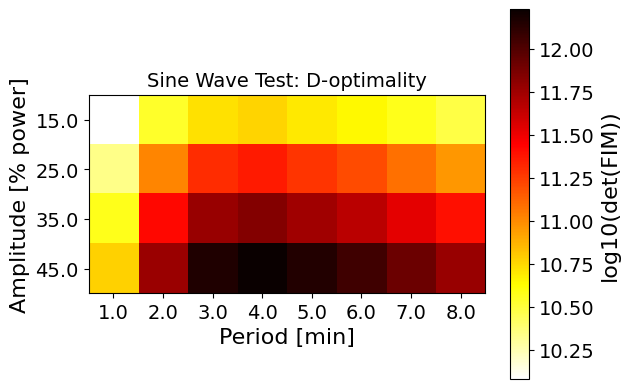
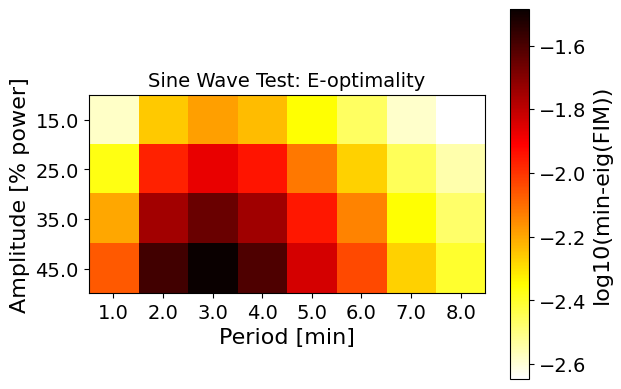
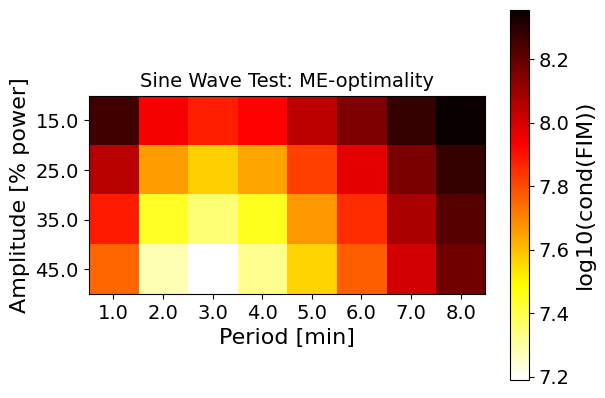
These heatmaps tell us a lot about the mathematical model for the TCLab system.
A-optimality (trace of FIM) is the largest with a long period (8 minutes) and large amplitude (45%). Why does this make sense? The long period means the heating and cooling is more gradual. This gives more information about the dynamics of the system, especially the lag in heat transfer between the two modeled thermal masses. Likewise, the larger amplitude ensures a larger temperature range is explored, which maximizes the ratio of the signal to noise (which is assumed to be i.i.d.)
The D-, E-, and modified-E optimality results are more nuanced. Even with the poorly identifiable parameter, we are still able to see that choosing a period of approximately 3 minutes is best for E- and ME-optimality, where D-optimality sees an optima at about 4-5 minutes of period.
One thing is consistent between all the optimality metrics: larger amplitude (toward 45%) results in more information.

